Politikk og samfunn

Gode på matematikk, dårlige på statistikk?

Sigve Indregard

tirsdag 17. august 2010 kl. 09:00

1997 ord

Norsk matematikkråd publiserer annet hvert år en undersøkelse som får stor oppmerksomhet. Det er en forkunnskapstest av studentenes matematikkunnskaper, og den består av et lite oppgavesett som sendes ut til universiteter og høgskoler.

Prøven brukes av matematikkrådet konsekvent for å argumentere for viktigheten av matematikkopplæring, og det blir fremholdt at tilbakegangen har vært sterk. Men prøven er så befengt med metodiske svakheter at det er vanskelig å ta resultatene alvorlig.

Sammenligningen med åttiårene

I undersøkelsen presenteres det kontinuerlige linjediagrammer med utviklingen fra første gjennomføring i 1985 til og med 2009. Det ser veldig dårlig ut. Korrekt svar-prosenten har falt fra over 70 til rundt 50.

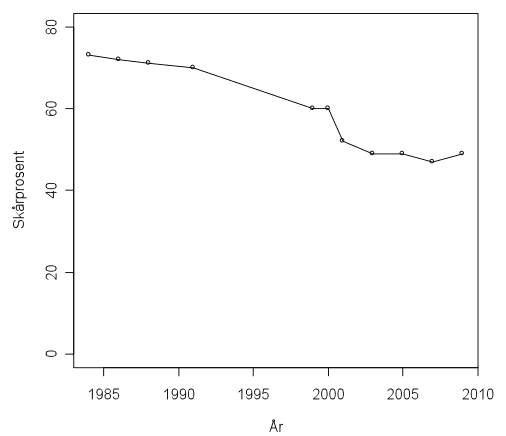
Bak dette diagrammet skjuler det seg tre problemer. For det første ble undersøkelsen gjennomført i 85, 87, 89 og 93 – men ikke mellom 93 og 99. For det andre har sammensetningen av respondenter endret seg betydelig fra de første gjennomføringene til de siste. For det tredje har testen endret seg – den ble revidert i 2000. Det er altså fullstendig meningsløst å sammenligne resultatene fra åttitallet og tidlig nittitall med de nye resultatene.

Hvis vi så kapper grafene på det saklige stedet, altså år 2000, står vi fremdeles igjen med noen feilkilder. Den viktigste feilkilden er at utvalget av studenter varierer sterkt fra år til år, uten at fordelingen oppgis i rapporten. Det eneste som oppgis er at det var betydelig flere realfagsstudenter i de første utvalgene (doh!). Den eneste måten å korrigere for dette tøvete utgangspunktet er å dele grunnlaget inn etter utdanning. Gjør vi det, forsvinner også teorien om at mattekunnskapene går tilbake:

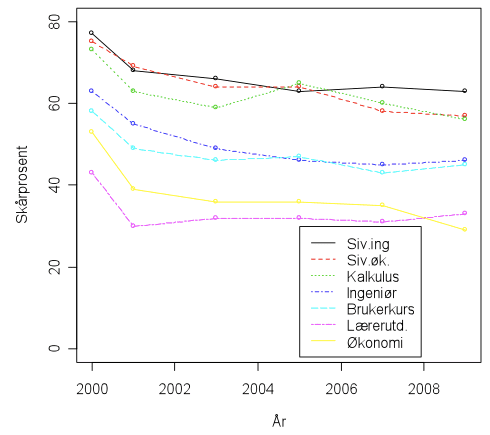
Hvis vi overser år 2000, som så vidt jeg kan forstå ble gjennomført med den gamle prøven, så har vi sett en klar forbedring blant lærerstudentene, og en svak tilbakegang på de andre matteintensive studiene. Basert på denne grafen er det betimelig å spørre seg hva alt maset er for, og spesielt hvorfor NMR i hver eneste pressemelding om dette drar frem lærerne.

Kjønn

NMR gjør den samme utvalgsfeilen når de presenterer gjennomsnittlig skår fordelt på kjønn. En kjapp titt på lista over utdanninger over viser hvorfor: fordelingen av antall studenter i utvalget fra de forskjellige utdanningene vil bestemme hvordan hvert kjønn gjør det. Tar man inn mange lærerstudenter, der det er mange kvinner, vil kvinnekarakteren bli trukket ned. Tar man derimot inn mange økonomistudenter, vil de kvinnene som er der trekke snittet relativt sett opp.

Den saklige måten å gjøre dette på har de faktisk gjort litt senere i undersøkelsen – tre sider etter at kapitlet om kjønn er ferdig. Grafen viser resultater fordelt på både kjønn og utdanning, og her forsvinner nesten all kjønnsforskjellen – men den er der fortsatt. I ingeniørutdanningen er kjønnsvariabelen nesten helt utvisket.

Kalkulatorbruk

NMR har over flere rapporter fremhevet en teori om at kalkulatorbruk medfører dårligere resultater i matematikk. I så fall burde ferdighetene gått mer tilbake jo mer kalkulator man brukte, men som vi har sett har resultatene vært nokså stabile på 2000-tallet. På den annen side var vel kalkulatorer godt tilgjengelige på nittitallet også; personlig husker jeg at vi hadde kalkulatorbegrensninger på ungdomsskolen (96-99), men ikke i videregående skole (99-02).

Selv om man kan vise til en korrelans mellom kalkulatorbruk og resultater, impliserer ikke dette noen årsakssammenheng. Det kan like godt være en tredje faktor som påvirker begge deler, eller en ren tilfeldig, spuriøs sammenheng. Det klassiske eksemplet er sammenhengen mellom pirater med sabler og global luftforurensing: da piratene forsvant, ble lufta forurenset. Det betyr imidlertid ikke at piratenes tilbaketog forårsaket luftforurensingen.

I stedet velger NMR følgende resonnement (fra 2007-rapporten):

Resultatene kan tyde på at hyppig bruk av kalkulator kan ha negativ innvirkning både på ferdigheter og begrepsforståelse. De som skårer best er de som sier at de bruker kalkulator relativt lite. Dette ser ut til å gjelde for alle utdanningsveier og er i samsvar med de funn en gjorde i 2005.

Selvrapportert bruk av kalkulator (på en skala fra ofte til sjelden) følger studentens skår på prøven nokså slavisk. Dette skyldes, i all hovedsak, at folk som er dårlige i matematikk oftere trenger hjelp til utregninger. Derav kalkulatoren. NMR foreslår vel ikke på den bakgrunn den tåpelige konklusjonen at det er kalkulatoren som gjør studentene svake? NMR ville fått samme resultater dersom de så på hvem som må ha hjelp av personalet for å bruke NSBs billettautomater, og følgelig konkludert med at det er togpersonalet som gjør folk til tekniske analfabeter. Eller de kunne ha sjekket sammenhengen mellom hvor ofte noen sjekker bruksanvisningen for å montere en del på en sykkel, og konkludert med skadeligheten av bruksanvisninger.

Denne måten å undersøke fenomenet gir på ingen måte grunnlag for å hevde at kalkulator skaper svakere grunnleggende ferdigheter i matematikk, en tese NMR har lagt til grunn når de har villet endre eksamensform, noe de har «arbeidet for i en årrekke». Det er selvsagt mulig at NMR har rett i at kalkulator er dumt. Men dette lar seg bare undersøke ved kontrollerte studier, eller pseudo-kontrollerte studier (f.eks. ved å undersøke effekten i land som endrer policy). NMR henviser bare til to artikler (Grønmo et.al. 2009a og Grønmo et.al. 2009b), og – lo and behold –* de sier faktisk ikke det NMR hevder de hevder.

Her er det NMR mener står i artiklene:

Grønmo (2009; 2009) setter den markante tilbakegangen i matematikkferdigheter i videregående skole i sammenheng med hyppig kalkulatorbruk.

Grønmo et. al. (2009a) handler ikke om videregående skole, men om grunnskolen. Som et siste punkt i en lang liste med mulige årsaker til gode og dårlige resultater i matematikk og naturfag:

Grønmo (2005) har, på basis av resultatene i TIMSS og PISA i 2003, argumentert for at grunnleggende ferdigheter i tall og tallbehandling er viktig for elevers utvikling av matematisk kompetanse. Hun hevder at en viss grad av automatisering av ferdigheter er nødvendig for at elevene skal utvikle denne kompetansen. For lite vekt på algoritmer og ferdigheter, som trening i multiplikasjonstabellen, vil kunne føre til at elevene ikke får opparbeidet det grunnlaget de trenger for å videreutvikle sine matematiske kunnskaper og ferdigheter.

Grønmo et. al. (2009b) handler faktisk om videregående skole, for å være nøyaktig studiespesialiserende elever med 3MX (noe som ikke er et krav for å komme inn på lærerskolen, forresten). Den nevner kalkulatorbruk noen steder blant mange andre årsaksforklaringer, og det nærmeste vi kommer NMRs påstand om innholdet er vel disse to sitatene:

Videre kan man peke på at det har vært en omfattende bruk av kalkulator og formelbok med egne notater det siste tiåret, som kan ha bidratt til mindre trening i – og vedlikehold av – ferdigheter som derivasjon…

Det er et tankekors at Slovenia og Italia, de to referanselandene med best resultat tatt i betraktning at de tester henholdsvis vel 40 % og 20 % av årskullet i TIMSS Advanced, er de to landene som synes å være mest tilbakeholdne med bruk av kalkulator. Tilsvarende tankevekkende er det at de to landene som har den mest markerte tilbakegangen fra forrige studie, Norge og Sverige, utmerker seg som to land som synes å bruke kalkulator mye.

Til dette er det å anføre at derivasjon ikke inngår i NMRs prøvesett, og at det siste resultatet knappast kan tas til inntekt for det veldig bastante sitatet over. TIMSS Advanced omfatter kun 3MX-klassene, og viser ganske riktig at norske lærere har lite trykk på automatisering og pugging av algoritmer, gangetabeller mm. Men at dette skal være på grunn av «hyppig kalkulatorbruk» fremstår som tendensiøst. Mer sannsynlig skyldes dette at læreplanene i Norge i liten grad legger vekt på pugging av algoritmer, gangetabeller mm. Det kan vi selvsagt diskutere, men å gjøre det om til en fordummende kalkulator-eller-ikke-debatt er et steg i feil retning.

Signifikante avvik fra god analyse av utvikling

Rapporten sier: «framgangen fra 2007 til 2009, som … er omtrent 1,5 %, er så liten at den ikke kan sies å være signifikant.» For det første har jeg vanskelig for å tro at det kan være riktig i en undersøkelse med over 5000 respondenter, i hvert fall med den behandlingen av data vi så langt har sett i rapporten, der alt bare klumpes sammen til en diger svarhaug.

For det andre oppgir de ikke noe sted hvordan de har regnet seg frem til det. For det tredje oppgir de ikke hvilke krav de setter til konfidens. Er det 90 %? 95 %? 99 %? Eller er vi på romferge-feilmarginer – 99,9 % konfidens?

For det fjerde nevnte ikke rapporten i 2007 noe om at nedgangen på 1,5 % ikke var signifikant. 2007-rapporten sa faktisk det stikk motsatte:

2007-undersøkelsen bekrefter at vi nå i enda høyere grad enn tidligere har studenter på de matematikkrevende kursene som i stor grad har et utilstrekkelig grunnlag i matematikk å bygge på for høyere utdanning.

Og videre:

Tilbakegangen er på 1,4 prosentpoeng i gjennomsnitt og kan ikke ses på som ubetydelig.

Moralen ser ut til å være at tilbakeganger på 1,4 prosentpoeng er «ikke ubetydelig», mens fremganger på 1,5 prosentpoeng er helt uten betydning. For å si det sånn: Dette vekker ikke min confidence. For meg ser det ut som om NMR har drevet data mining: De leter med lys og lykter etter tall og resultater som passer deres agenda, og overser glatt data som stritter mot.

Vi kan også regne ut om det er signifikant selv.

I rapporten ser vi at respondentenes skårer fordeler seg omtrent normalt rundt et gjennomsnitt på 21.37 poeng (av 44 mulige), med standardavvik på 9.554 og ca. 5500 respondenter. Med mindre andre forbehold trekkes inn er da et 95 % konfidensintervall lik:

21.37 \pm 1.96 \times \frac{9.554}{\sqrt{5500}} = 21.37 \pm 0.13

Vi er altså 95 % sikre på at det virkelige populasjons-gjennomsnittet ligger mellom 21.24 og 21.40, eller målt i prosent riktig, mellom 48.27 og 48.64 prosent. Forbedringen på 1.5 prosentpoeng er, med mindre noen andre forbehold trekkes inn, særdeles signifikant – nesten syv hele standardavvik betyr at resultatet er signifikant på mer en 99.99999 %-nivået.

Det forfatterne trolig har tenkt, er at konfidensintervallene blir større på grunn av a) dårlig sampling (uvisst om det er et tilfeldig utvalg) og b) dårlig stratifisering (utdanningsgruppene i undersøkelsene endrer kronisk størrelse). Det som er underlig, er at disse forbeholdene ikke forklares og ikke tas i andre sammenhenger. Hvis de faktisk mener dette, viser undersøkelsen nøyaktig ingenting - sterkt i strid med det tidligere rapporter har hevdet. Til 2009-rapportens forsvar skal det sies at den er meget forsiktig med å hevde noe som helst om hva resultatene betyr.

På dette tidspunktet måtte jeg nesten sjekke hvem de oppgitte forfatterne er. I 2009-rapporten er de en stipendiat ved institutt for spesialpedagogikk (UiO), en førsteamanuensis i matematikk og statistikk (UiT) og en professor i matematikk (UiO). De er alle tre styremedlemmer i Matematikkrådet. I 2007-rapporten var de en høgskolelektor og en førsteamanuensis som driver matematikkopplæring for lærere, begge fra HiT. Jeg velger å la den interesserte leser sjekke opp navnene selv, dersom det har interesse.

Konklusjon

Matematikkrådet får karakteren 2. Selv om innsatsen og engasjementet holder til en femmer, må den usaklige ekstrapoleringen av råskårene fra undersøkselsen trekke kraftig ned. Et råd for matematikk bør ha statistiske grunnregler under huden, og matematikklærere med statistisk bakgrunn kan umulig være bekjent av rapportens innhold.

Jeg er veldig bekymret for at denne typen lettvint synsing om norsk skole bygger opp et bilde av den norske skolen i totalt forfall. Det er ingen undersøkelser som tyder på at norske studenter i 19-årsalderen er vesentlig dårligere rustet enn tidligere. Det er derimot mye annet spennende i undersøkelsene. Mye tyder på at norske barn kommer sent i gang med læring av grunnferdigheter, og mye tyder på at vi svikter de svakeste.

Det er forøvrig godt mulig at rådet har rett i at norske studenter har svake eller svakere matematikkferdigheter. Problemet er at en slik god sak aldri bør fremmes ved tendensiøs bruk av statistikk, der tallene attpåtil viser noe annet enn det hovedbildet NMR trekker frem i pressemeldinger og intervjuer. Det er rett og slett for lett for alle som har liten entusiasme for matematikk å overse denne typen agitasjon.

Kilder:

Fortsatt dårlige i matte, ap.no, 16. august
Rapporten for 2009 (pdf) (pdf)
Rapporten for 2007 (pdf)