Meningsmålermeningsmåling

Vi er vant til at meningsmålinger ikke er nøyaktige. I det siste har meningsmålerne svart på deler av kritikken. En av svarene har vært å oppgi feilmarginer.

Sofistikerte politiske kommentatorer husker alltid på å nevne dette før de gyver løs med overdrevent sikre konklusjoner basert på dagens måling. «Selv om bevegelsene er innenfor feilmarginene…». Men hvor sikre er egentlig disse feilmarginene?

I dag har vi fått tre målinger av Høyre: én på 33,0 (± 2,9), én på 29,2 (± 2,8) og én på 37,6 (± 3,0). Feilmarginen skal angi et intervall der det, ut fra resultatene i målingen, er 95 % sikkert at partiets virkelige oppslutning ligger innenfor intervallet.

Slik ser det ut hvis vi setter opp sannsynlighetskurvene (tetthetskurver) for de tre forslagene. Legg merke til at det er svært lite overlapp: steder der det er særlig sannsynlig at den virkelige oppslutningen ligger som gjør både den rød, grønne og blå målingen riktig.

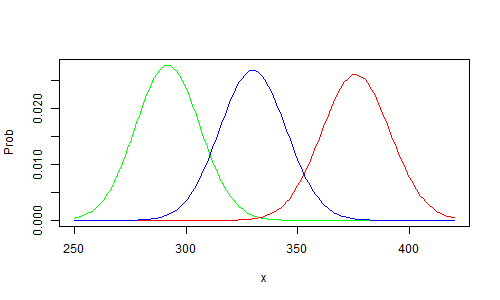
La oss nå anta at meningsmålerne har korrekte metoder for å måle hva folk kommer til å stemme i valg. Vi antar også at de legger til grunn det samme folket, altså at det er den samme, sanne, underliggende prosentsatsen av velgere som vil stemme Høyre. Videre antar vi at metoden for å sette feilmargin og sikkerhet i analysen er korrekt (estimere reliabilitet). Hva er da sannsynligheten for at dagens hendelser skulle inntreffe?

Matten er litt komplisert¹, men svaret er enkelt: Sannsynligheten for at dette skulle oppstå ved en tilfeldighet er omtrent én til tre hundre tusen: 0.000003. Det er en forsvinnende liten sannsynlighet. Det er som å strø en desiliter sukker ut på gulvet, og så plukke opp et eneste sukkerkorn, og få det riktige kornet.

Det er altså høyst sannsynlig noen som tar feil, og enda viktigere: det er svært usannsynlig at feilmarginene er riktig satt.

Vi begynte med å anta at meningsmålerne har korrekte metoder. Vi har funnet at dersom metodene er korrekte, er dagens resultater ekstremt lite sannsynlige. Vi kan konkludere, med stor grad av sikkerhet, at minst ett av instituttene enten ikke har valide metoder, eller at de ikke er så reliable som feilmarginen antyder.

Her er forklaringen på at det kan skje:

Målefeil kan oppstå på grunn av tre helt ulike feilkilder. Den første er den vanlige, som de fleste forbinder med feilmargin, og som er det disse beregnede feilmarginene gir uttrykk for. Hvis du spør ti tilfeldige mennesker på gaten, vil du selvsagt ikke få et representativt uttrykk. Du vil få en skår (en statistikk, som det heter på fagspråket) som har knyttet til seg en viss usikkerhet. Dersom du vet hvor mange du har spurt, kan denne usikkerheten måles og kvantifiseres. Jo flere du spør, jo mindre blir usikkerheten.

Det er denne typen usikkerhet - og bare det - som danner grunnlag for feilmarginen meningsmålerne oppgir. De antar altså, implisitt, at de har et perfekt randomisert utvalg og en perfekt, valid og reliabel metode for å finne ut hva folk kommer til å stemme - og hvem som faktisk ender opp med å stemme - gjennom et telefonintervju.

Den andre usikkerheten skyldes svakhet i utvalget. La oss si at du bare spør de ti som du møter først. Det er ikke et representativt utvalg: du vil trolig møte en familie, eller i hvert fall folk som er ute og går samtidig, og ikke minst folk som bor i nærheten av der du er. Slike feil fører til forskyvinger i tallmaterialet.

Også slike ting er i prinsippet kvantifiserbare, men i praksis er det veldig vanskelig, fordi du aldri vet om alle de relevante faktorene å trekke inn. Den beste måten å unngå den andre feilen, er å bruke et helt tilfeldig utvalg.

Her er ikke meningsmålerne perfekte. Det er nemlig ikke tilfeldig hvem som svarer på telefon, hvem som har telefon, hvem som svarer instituttet, osv. Målerne forsøker å korrigere for dette ved å legge på vekter avhengig av forskjellige parametre. Har de for få ungdommer i det utvalget de fikk i dag, multipliserer de opp svarene til de ungdommene som faktisk svarte. Men i og med at målerne ikke kjenner alle relevante kriterier befolknigen fordeler seg etter, er det umulig å bli helt kvitt den ekstra usikkerheten som følger av ikke-randomiserte utvalg.

Men det finnes også en tredje: metodesvakheter. Det er to hovedsvakheter for meningsmålinger. Den ene er at folk ofte ikke stemmer, og det er ikke jevnt fordelt mellom partiene. Den andre er at folk ikke er ærlige når de blir intervjuet, og det er heller ikke tilfeldig.

Effektene av dette er uoversiktlige og vanskelige å kvantifisere. Man forsøker seg på å avstemme det hele ved å gjøre råmålinger omtrent samtidig som valg, og se hvordan målingen avviker fra fasit. Deretter korrigerer man med en fast faktor: er det slik at råmålingen viser at Frp måles 11 % for høyt, ganger man Frps tall med dette fra da av.

Men dette introduserer usikkerhet: disse faktorene kan endre seg i løpet av året. De kan flytte seg fra parti til parti. Ulike velgergrupper kan mobiliseres og demobiliseres. Fordi meningsmålingsinstituttene har ulike måter å vekte på, vil dette slå ulikt ut. Jeg kjenner ikke detaljene i vektingsystemene de bruker, men det er ikke utenkelig at det også vil slå ulikt ut i løpet av tiden mellom to valg. Kanskje bruker noen vektingsformler som tar høyde for at Høyrebølgen vi ser nå er en type svingning som sjelden manifesterer seg i valg, og justerer dem ned?

Uansett vil disse feilene øke usikkerheten knyttet til en måling, uten at det er tatt med i det enkle målet på usikkerhet som målingene oppgir.